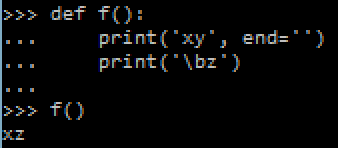
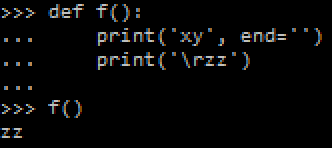
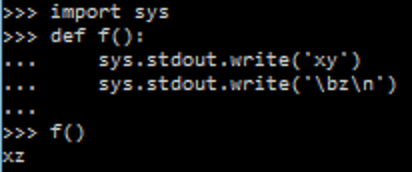
Polynomials are great. They're a simple mathematical equation pattern which is simple and easy to work with. You basically have a number of constants "a", "b", "c", etc. which you use in the following pattern:
f(x) = a x^0 + b x^1 + c x^2 + ...
By changing the values of the constants you change the shape of the graph of f(x). You can design a particular graph shape by choosing the values of these constants. In fact, one of the most interesting properties of polynomials is that they can be easily designed so that their graph passes exactly through a given set of points. For example, you can choose the constants of the polynomial to make f(1) = 2, f(3) = -1, f(-1.5) = 0.5, etc. This is very easy to make using
Lagrange polynomials. The constants of the polynomial can be seen as parameters which can be optimized in order to get a desired function.
Polynomials are not the only equation which is designed to be easily modifiable. One of the most well known modifiable equation patterns are
Artificial Neural Networks. Although neural networks are inspired by the neurons in the brain and how they change when learning to perform new tasks, the concept behind neural networks is that of having an equation that, by design, can be easily modified to turn chosen inputs into chosen outputs. They can take any number of inputs and outputs and they usually only work on binary numbers (which is great for computers). They have been used for lots of things such as recognising objects in images and classifying text into meaningful categories. Neural networks are known to generalise a set of input-output mappings into useful functions that work well for new inputs. For example, if you design a neural network to map 100 particular pictures of dogs to the output "1" and another 100 particular pictures of cats to the output "0", then the network will start giving the expected output for new pictures of dogs and cats.
Neural network definition
Whereas the building block of the polynomial is the term "k x^i", the building block of the neural network is the neuron. A neuron takes in a number of signals from other neurons, weighs the signals by their importance by making them weaker or stronger, adds them together and if the sum is over a particular threshold, then the neuron will output its own signal to some other neurons. Here is a diagram of this:

Neurons are organized into layers, where one layer of neurons supplies input signals to the next layer of neurons. In mathematical terms, a neuron is defined as follows:
 Activation functions
Activation functions are functions that sharply change value when the input is over a certain threshold. Traditionally, neural networks use the sigmoid function given above which has a graph like this:

See how the value changes from 0 to 1 after passing x = 0? This is what will make the neuron output a signal if the weighted sum is over a threshold. Left as is, the threshold is 0; but we can change the threshold by changing the value of the bias in order to shift the graph to the left or right. The weighting of input signals by importance is done by multiplying the input by a weight, which can be a large number, a small fraction, or even a negative number.
Just like you can modify polynomial functions by changing their constants, you can modify neural network functions by changing their weights and biases. Further down we'll see how to do this.
Neural network example
Given the above definitions, here is a diagram of an example of a neural network:

We shall be referring to this diagram throughout this blog post. Notice the following things about it:
- Its 2 inputs are called "x0" and "x1" whilst its 2 outputs are called "y0" and "y1".
- Since there are two outputs, the output of the whole network is a column vector of two numbers.
- The first layer of neurons are square because they propagate the "x" signals to the next layer unmodified. The rest of the neurons work as explained.
- Each circle neuron receives input signals from all neurons in the previous layer.
- Apart from input signals, each circle neuron also accepts a bias signal that is always the same.
This diagram is just a visual representation of the equation shown below. The equation is derived layer by layer from the output. Notice how the equation is a column vector of two numbers since there are two outputs.

Notice that we are representing the neural network using normal algebra instead of using linear algebra with matrices as usual. I believe that this makes the example easier to understand. Linear algebra is useful for generalising the concepts to any neural network shape, but for understand one network example we'll stick to this expanded representation.
Neural network modification
So now we know how to create a neural network equation, but how do we choose its weights and biases in order to get the function we want? In the
previous blog post, we talked about how to use the gradient descent algorithm in order to numerically find the minimum of an equation when solving the equation algebraically is difficult. In fact, one of the most well known uses of the gradient descent algorithm is for "training" neural networks into performing a desired function, that is, giving desired outputs from particular inputs.
Usually neural networks are trained using the
backpropagation algorithm which is based on the gradient descent algorithm. However we'll see how to do the training using plain gradient descent which will help us understand the backpropagation algorithm in a later blog post.
What we'll do is create a "cost" function that quantifies how close the outputs that the network is giving are to the desired outputs. Suppose that we want the above neural network to output (0,1) when given (0,0) and (1,0) when given (1,1). The cost function will measure how far off the neural network is from actually giving these outputs. If the cost function gives 0, then the network is giving exactly these desired outputs, otherwise it will be larger than zero. Different weights and biases will make the cost function give different values and our job is to find the combination of weights and biases that will give a cost of zero. We will do this using the gradient descent algorithm.
There are many possible cost functions, but traditionally, this is how we define the cost function:

Notice that O(X,W,B) = Y.
The cost function here is measuring how far the actual output is from the target output by calculating the
mean squared error. For convenience later on we're also dividing the equation by 2.
For the above network, the cost function applies as follows:

Now that we have a continuous equation that quantifies how far from the desired function our neural network's weights and biases are, we can use gradient descent in order to optimize the weights and biases into giving the desired function. To do that we need to find the partial derivative of the network's equation with respect to every weight and bias. Before we do so, notice that the derivative of the activation function is as follows:

The above equation is saying that the derivative of a neuron's output is defined using the neuron's output (the output multiplied by one minus the output). This is a useful speed optimization in sigmoid activation functions.
We shall now find the partial derivative of two weights and two biases. You can then find the partial derivatives of every other weight and bias yourself. Make sure that you know how the
chain rule in differentiation works. As you follow the derivations, keep in mind that all the "y"s and "n"s are actually functions of "B", "W", and "X" just like "O", but we'll leave the "(X,W,B)" out in order to save space.
Partial derivative with respect to weight in layer 3 (output layer)
Let's find the partial derivative of one of the weights in layer 3 (output layer).

Notice how the 2 in the denominator was cancelled with the 2s in the numerator. This is why we put it in the denominator of the cost function. Notice also that the summation does not change anything in the derivative since the derivative of a summation is the summation of the summed terms' derivative.
Now we'll find the derivative of each "y" separately.

Notice that we stopped decomposing neurons past layer 3 since we know that the weight we are deriving with respect to will not lie in deeper layers.
Finally we plug these back into the original equation and we have our partial derivative:

It's important to notice that the derivative uses the output of the network's neurons. This is important, since it means that before finding the derivative we need to first find the output of the network. Notice also that the green "n" at layer 3 is "y0" but we won't replace it with "y0" in order to preserve a pattern that is revealed later.
Partial derivative with respect to bias in layer 3 (output layer)
Let's find the partial derivative of one of the biases in layer 3 (output layer) now. We'll skip some steps that were shown in the previous derivations.

And now we find the derivatives of the "y"s separately.

And we now plug them back into the original equation.

Partial derivative with respect to weight in layer 2
Let's find the partial derivative of one of the weights in layer 2 now. We'll skip some steps that were shown in the previous derivations.

And now we find the derivatives of the "y"s separately.

And we now plug them back into the original equation.

Partial derivative with respect to bias in layer 2
Let's find the partial derivative of one of the biases in layer 2 now. We'll skip some steps that were shown in the previous derivations.

And now we find the derivatives of the "y"s separately.

And we now plug them back into the original equation.

Partial derivative with respect to weight in layer 1
Let's find the partial derivative of one of the weights in layer 1 now. We'll skip some steps that were shown in the previous derivations.

And now we find the derivatives of the "y"s separately.

And we now plug them back into the original equation.

Notice that we did not replace the black "n" at layer 0 with "x" in order to preserve a pattern that is revealed later.
Partial derivative with respect to bias in layer 1
Let's find the partial derivative of one of the biases in layer 1 now. We'll skip some steps that were shown in the previous derivations.

And now we find the derivatives of the "y"s separately.

And we now plug them back into the original equation.

Patterns
There is a pattern in the derivatives. In order to see the pattern, let's look at a part of the equation inside the summations of all the derivatives and compare them.
Here is the repeating pattern in the derivation for the weights:

Here is the repeating pattern in the derivation for the biases:

See how there is a repeating pattern that gets longer as the layer of the weight we are deriving with respect to gets deeper into the network? This is an important pattern on which the backpropagation algorithm is based, which computes the gradient of a layer's weights using the gradients of the previous layer.
Notice also that as more layers are added, the chain of multiplications gets longer. Since each number is a fraction between 0 and 1, the multiplications produce smaller and smaller numbers as the chain gets longer. This will make the gradients become smaller which makes training the layers at the back very slow. In fact this is a problem in multi-layered neural networks which is known as the
vanishing gradient problem. It can be solved by using different activation functions such as the
rectified linear unit.
In code
Now that we know how to find the partial derivative of every weight and bias, all we have to do is plug them in the gradient descent algorithm and minimize the cost function. When the cost function is minimized, the network will give us the desired outputs.
Here is a complete code example in Python 3 of a gradient descent algorithm applied to train the above neural network to act as a half adder. A half adder adds together two binary digits and returns the sum and carry. So 0 + 1 in binary gives 1 carry 0 whilst 1 + 1 in binary gives 0 carry 1. One of the functions is called "ns" which gives the outputs of each neuron in the network given an input, grouped by layer. This will be called several times by the gradient functions, so to avoid recomputing the same values, it's output is automatically cached by Python using the lru_cache decorator. The initial values are set to random numbers between 1 and -1 since starting them off as all zeros as was done in the previous blog post will
prevent the gradient descent algorithm from working in a neural network.
import math
import random
from functools import lru_cache
trainingset = { (0,0):(0,0), (0,1):(1,0), (1,0):(1,0), (1,1):(0,1) }
def grad_desc(cost, gradients, initial_values, step_size, threshold):
old_values = initial_values
while True:
new_values = [ value - step_size*gradient(*old_values) for (value, gradient) in zip(old_values, gradients) ]
if cost(*new_values) < threshold:
return new_values
old_values = new_values
def a(z):
return 1/(1 + math.exp(-z))
@lru_cache(maxsize=4)
def ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
(n00, n01) = ( x0, x1 )
(n10, n11) = ( a(n00*w100 + n01*w110 + b10), a(n00*w101 + n01*w111 + b11) )
(n20, n21) = ( a(n10*w200 + n11*w210 + b20), a(n10*w201 + n11*w211 + b21) )
(n30, n31) = ( a(n20*w300 + n21*w310 + b30), a(n20*w301 + n21*w311 + b31) )
return ( (n00, n01), (n10, n11), (n20, n21), (n30, n31) )
def out(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
return ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)[-1]
def cost(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
(y0, y1) = out(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
tmp += (y0 - t0)**2 + (y1 - t1)**2
return tmp/(2*len(trainingset))
def dCdw300(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * n30*(1-n30) * n20
return tmp/len(trainingset)
def dCdw310(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * n30*(1-n30) * n21
return tmp/len(trainingset)
def dCdw301(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y1 - t1) * n31*(1-n31) * n20
return tmp/len(trainingset)
def dCdw311(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y1 - t1) * n31*(1-n31) * n21
return tmp/len(trainingset)
def dCdb30(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * n30*(1-n30)
return tmp/len(trainingset)
def dCdb31(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y1 - t1) * n31*(1-n31)
return tmp/len(trainingset)
def dCdw200(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*n10 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*n10 ))
return tmp/len(trainingset)
def dCdw210(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*n11 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*n11 ))
return tmp/len(trainingset)
def dCdw201(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w310*n21*(1-n21)*n10 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w311*n21*(1-n21)*n10 ))
return tmp/len(trainingset)
def dCdw211(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w310*n21*(1-n21)*n11 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w311*n21*(1-n21)*n11 ))
return tmp/len(trainingset)
def dCdb20(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20) ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20) ))
return tmp/len(trainingset)
def dCdb21(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w310*n21*(1-n21) ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w311*n21*(1-n21) ))
return tmp/len(trainingset)
def dCdw100(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*w200*n10*(1-n10)*n00 + w310*n21*(1-n21)*w201*n10*(1-n10)*n00 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*w200*n10*(1-n10)*n00 + w311*n21*(1-n21)*w201*n10*(1-n10)*n00 ))
return tmp/len(trainingset)
def dCdw110(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*w200*n10*(1-n10)*n01 + w310*n21*(1-n21)*w201*n10*(1-n10)*n01 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*w200*n10*(1-n10)*n01 + w311*n21*(1-n21)*w201*n10*(1-n10)*n01 ))
return tmp/len(trainingset)
def dCdw101(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*w210*n11*(1-n11)*n00 + w310*n21*(1-n21)*w211*n11*(1-n11)*n00 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*w210*n11*(1-n11)*n00 + w311*n21*(1-n21)*w211*n11*(1-n11)*n00 ))
return tmp/len(trainingset)
def dCdw111(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*w210*n11*(1-n11)*n01 + w310*n21*(1-n21)*w211*n11*(1-n11)*n01 ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*w210*n11*(1-n11)*n01 + w311*n21*(1-n21)*w211*n11*(1-n11)*n01 ))
return tmp/len(trainingset)
def dCdb10(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*w200*n10*(1-n10) + w310*n21*(1-n21)*w201*n10*(1-n10) ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*w200*n10*(1-n10) + w311*n21*(1-n21)*w201*n10*(1-n10) ))
return tmp/len(trainingset)
def dCdb11(w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31):
tmp = 0
for ((x0,x1), (t0,t1)) in trainingset.items():
( (n00, n01), (n10, n11), (n20, n21), (n30, n31) ) = ns(x0, x1, w100, w101, w110, w111, b10, b11, w200, w201, w210, w211, b20, b21, w300, w301, w310, w311, b30, b31)
(y0, y1) = (n30, n31)
tmp += (y0 - t0) * ( n30*(1-n30) * ( w300*n20*(1-n20)*w210*n11*(1-n11) + w310*n21*(1-n21)*w211*n11*(1-n11) ))
tmp += (y1 - t1) * ( n31*(1-n31) * ( w301*n20*(1-n20)*w210*n11*(1-n11) + w311*n21*(1-n21)*w211*n11*(1-n11) ))
return tmp/len(trainingset)
new_values = grad_desc(
cost,
[ dCdw100, dCdw101, dCdw110, dCdw111, dCdb10, dCdb11, dCdw200, dCdw201, dCdw210, dCdw211, dCdb20, dCdb21, dCdw300, dCdw301, dCdw310, dCdw311, dCdb30, dCdb31 ],
[ 2*random.random()-1 for _ in range(18) ],
0.5,
1e-3
)
print('cost:', cost(*new_values))
print('output:')
for ((x0,x1), (t0,t1)) in trainingset.items():
print(' ', (x0,x1), out(x0,x1,*new_values))
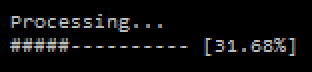
Wait a few seconds and...
cost: 0.0009999186077385778
output:
(0, 1) (0.9625083358870274, 0.02072955340806345)
(1, 0) (0.9649753465406843, 0.02060601544190889)
(0, 0) (0.03678639641748687, 0.0051592625464787585)
(1, 1) (0.04304611235264617, 0.9642249998318806)
Conclusion
Of course this isn't a very convenient way to train neural networks since we need to create a different set of partial derivatives for every new network shape (number of neurons and layers). In fact, in a future blog post we'll see how to use the backpropagation algorithm which exploits patterns in this process in order to simplify the process. On the other hand, the backpropagation algorithm makes certain assumptions about the network, such as that every neuron in a layer is connected to every neuron in the previous layer. If we were to make no assumptions about the network then we'd end up using the bare bones method presented here.