I remember back when I was in school when, during physics lessons on motion, we would have velocity-time graphs of some car, where the graph tells you how fast the car was going at any given time, like the one below:
So this is saying that the car started from rest (0m/s) then it accelerated to 20m/s, and so on. The interesting part about this is that you can apparently find the distance travelled by the car by finding the area under the graph. Now eventually I learned that this is because the area under the graph is equal to the anti-derivative of the graph which makes transforms the velocity-time graph back into a distance-time graph (since the derivative of the distance-time graph is the velocity-time graph). But back when I was doing this thing in school we didn't know about calculus so we were not given a reason for why this works, which is a shame because you actually don't need calculus if you're not dealing with curves.
So why does this work? Well, in order to find the area under the graph you need to first break it up into a set of basic shapes as below. Triangles, rectangles, trapezia, and so on. You then find the area of each individual basic shape and find the total.
Let's start with the rectangle. Why is the area under a rectangle equal to the distance travelled? A rectangle means that the velocity for a period of time was constant. The width is the duration and the height is the velocity.
Now if the car was travelling at a constant speed of $v$ for duration $t$, what is the distance travelled? If $v = s/t$ then $s = vt$, that is, the distance travelled is the velocity multiplied by the duration, which just so happens to be the area of the rectangle.
Now one important thing to note about all the sub-shapes under the graph is that they are all different forms of trapezia. A trapezium with equal sides is a rectangle and a trapezium with one side being zero is a triangle. So we can focus on just the trapezium.
So now we can't just use the equation $v = s/t$ because that assumes that the velocity is constant, whereas here it has increased (steadily) from $v_1$ to $v_2$. Now without referring to Newton's equations of motion, it is clear that there exists a single constant velocity which is between $v_1$ and $v_2$ such that the distance travelled in the same duration is equal to the distance travelled after this acceleration. In other words, there is some rectangle with a height that is between $v_1$ and $v_2$ that should give the same answer. We usually call this height the average velocity and it is usually found by dividing the total distance travelled by the total duration of travelling. But here we don't have the distance travelled, only the initial and final velocity. So what is the average velocity of a uniformly increasing velocity?
The answer is the average height of the trapezium, which is $(v_1 + v_2)/2$. We can convince ourselves that this is the average height of the trapezium by sampling a number of points along the top side of the trapezium and finding what the average of the sample heights is. Let's take trapezium C in the brokendown graph above which is between time 20 and 25:
Of course since this is just a single case you might not be convinced yet; so let's do this algebraically using a variable amount of samples $n$:
$$ \hat{v} = \frac{\sum_{i \in 0...n-1}{(v_1 + \frac{i\times(v_2 - v_1)}{n-1})}}{n} \\ \hat{v} = \frac{\sum_{i \in 0...n-1}{v_1} + \sum_{i \in 0...n-1}{\frac{i\times(v_2 - v_1)}{n-1}}}{n} \\ \hat{v} = \frac{n v_1 + \frac{(v_2 - v_1)\times\sum_{i \in 0...n-1}{i}}{n-1}}{n} \\ \hat{v} = v_1 + \frac{(v_2 - v_1)\times\sum_{i \in 0...n-1}{i}}{n\times(n-1)} \\ \hat{v} = v_1 + \frac{(v_2 - v_1)\times\frac{n\times(n-1)}{2}}{n\times(n-1)} \\ \hat{v} = v_1 + \frac{v_2 - v_1}{2} \\ \hat{v} = v_1 + \frac{v_2}{2} - \frac{v_1}{2} \\ \hat{v} = \frac{v_2}{2} + \frac{v_1}{2} \\ \hat{v} = \frac{v_2 + v_1}{2} $$Great! So now we know that given a trapezium of velocity-time graph, this is equivalent to a rectangle of the same width but with a height that is the average of the two sides:
We already know how to find the distance travelled by a rectangle shaped velocity-time graph so let's use it on the above rectangle: $s = (v2+v1)/2\times t$. It just so happens that this is also the area of the trapezium. So we can just skip all the above and just take the area of the trapezium to find the distance travelled.
All that's left is what is the distance travelled when the velocity is zero since it's just a flat line, but I'm sure you can guess what that is.





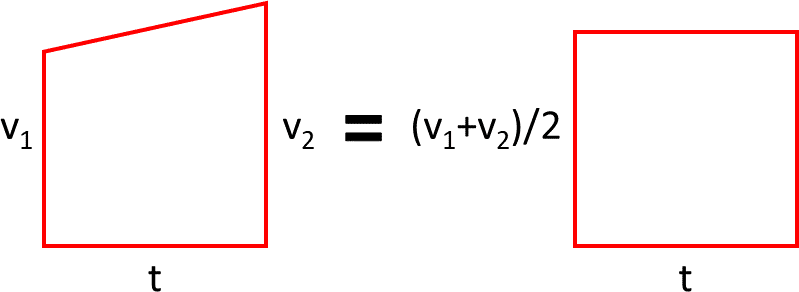
No comments:
Post a Comment